Tetrahedral coordinates - mathematical elaboration

A fractal 'Sierpinski tetrahedron' metal sculpture in Breckenridge, Minnesota
credit: Breckenridge Senior High Mathletes
A tetrahedral system for defining co-ordinates in all-space has been proposed by me in 1996 in Tetra Space Co-ordinates. My proposal was roughly time coincident but independent from discussions and mathematical elaborations on 'Quadray coordinates' taking place between David Chako, Tom Ace and Kirby Urner. The outline of their ideas and some links can be found in a Wikipedia article titled Quadray Coordinates.
The idea of basing all-space coordinates on tetrahedral geometry instead of the Cartesian right-angle X-Y-Z axes goes back to Buckminster Fuller. It is conceptually sound but it needs mathematical elaboration to become useful for general application. The maths should be simple and of immediate applicability, which is quite a challenge. We have all been brought up with a system of coordinates that today is in exclusive use, leaving little space for a different idea...
Cartesian coordinates
Today's Cartesian co-ordinates proceed from a point in space, giving origin to three directions or vectors, the X, Y and Z axes, which are arranged in 90-degree co-ordination. Those axes define one of the angles of a cubic section of space. By establishing distances along each one of the three axes, a point in space can be determined. Those co-ordinates work well in a setting of space where a cube or cuboid-shaped volume is to be described, however it gets more complicated when describing all-space, that is, any conceivable direction of the spherical extension we call space. In combination with the subdivision of a complete circle into 360 degrees, where 90 degrees is exactly one quarter, we may, in the Cartesian system, define the space around us with reference to six vectors: up, down, east, west, north, south. Each of those vectors is separated by 90 degrees from its four nearest neighbors, and by 180 degrees from its negative 'twin'.
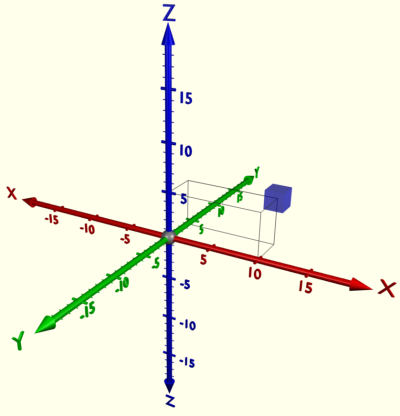
Cartesian Coordinates - image credit: rab3d - Blender
To describe any direction in space, we must first establish a horizon, cutting the spherical volume in two. Choosing one of the two half-spheres, we can define which way is up (above our horizon) or down (below our horizon). A direction or exact vector can now be defined with reference to the 360 degree subdivision of the circumference of the horizon, and an elevation from horizon towards the vertical expressed in degrees. For increased accuracy, each degree may be subdivided into 60 minutes and each minute into 60 seconds.
The system worked rather well as long as we stayed on the surface of the earth, navigating the seas, where the horizon is naturally established by the existing vertical (downward directed) vector of gravitation. It is not optimal however for describing all-space.
So pervasive has the Cartesian coordinate system become in our culture, that its X-Y-Z axes have taken on the meaning of "dimensions". Each one of the right-angle axes of the system is thought to denote a dimension with physical meaning. We are describing our world as "three dimensional".
I suspect that in reality, physical extension (in all directions) should be called a dimension of physical space, and time should probably also have the distinction of being a dimension. There is no compelling reason to see the axes of a coordinate system as inherent in the make up of the physical universe and call them dimensions.
A different geometry of 'dimensions'
In a space setting, tetrahedral co-ordinates have the potential to considerably simplify orientation and navigation. Tetrahedral co-ordinates are based on four principal axes. For the sake of convenient description, the four tetrahedral axes are defined as having their origin at the central point of an imaginary tetrahedron, each one exiting at one of the four vertices. (This is different from my original proposal, where the tetrahedral axes were said to exit at the center of a face. Note that both systems are possible.) Our imaginary tetrahedron may be situated at any preferred point of observation. It may be oriented with reference to an external fixed point, such as a distant star system or a galaxy, or with regard to a vehicle (satellite, space ship) in free space. It may also co-rotate with a sphere such as a planet or a star, for instance the sun.
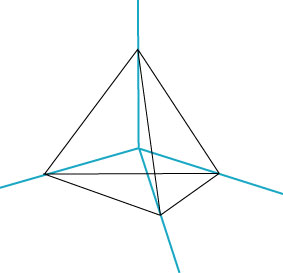
Without the need for an artificial horizon, we can now define any imaginable direction in space - starting from the point of origin - by reference to three of those tetrahedral axes. Since we are dealing with a natively spherical system of orientation, our old subdivision of the circle into degrees, minutes and seconds is no longer an optimal system for describing the relation of any vector to the three principal tetrahedral axes that delimit the "sector" containing the direction we wish to describe. Note that the entire sphere has been subdivided into four sectors, each one delimited by three of the tetrahedral axes. For the sake of simplicity, each sector may be seen as corresponding to one of the faces of the tetrahedron. In reality however, we are describing points on the surface of a sphere.
Expressed in our present 360-degree-system, the angle between each one of the four tetrahedral axes is an awkward and only approximately accurate 109.4712 degrees. Therefore, in order to fully utilize the potential of this tetrahedral system of all-space orientation, we will need a different subdivision from the 360-degree horizon and the 90-degree "right" angle of the old X-Y-Z Cartesian system.
Two possibilities come to mind...
- - -
We can describe distances from each of the axes that delimit a sector, as a number from zero to 100 (a percentage of distance) to pinpoint an exact direction using three of those distance measurements, or we can subdivide the sector's curved triangular surface area into ever smaller triangles, which will enable us to indicate, with increasing precision, the direction we are seeking to define.
Our description, in both cases, will have to follow not the flat face of the imaginary tetrahedron, but the curved topology of a sphere enclosing the space out to a specified distance from the point of origin. Thus, in order to define any point in surrounding space, all we will need is an indication of distance from origin, and a definition of the exact direction in one of four sectors, further defined with reference to three of the four principal axes of the tetrahedron.
Color coding vs. Fractal granularity
Each one of the four axes of the tetrahedron indicating a principal direction could be assigned one of four principal colors. In my earlier proposal I chose the four colors of the printing process - cyan, magenta, yellow and black (CMYK), which in their various mixtures of percentage can express a palette of millions of individually different colors, allowing orientation not only by number but also - in a more intuitive way - by color. CMYK is probably not the only and perhaps not even the best color combination that may be used. The method of percentage to describe a vector is easy to use with the color coding of the sphere's surface. Computer software is quite capable of assigning the resulting unique color to any of millions of different directions.
The following image by Kirby Urner depicts the basic idea, although in a less-than-perfect way. The edges of the tetrahedron, colored in one solid color which is a mix of the colors of the two axes they touch, should be a continuous color gradient from one solid color to the other, with only the midpoint of the edge in the color the whole edge is shown in.
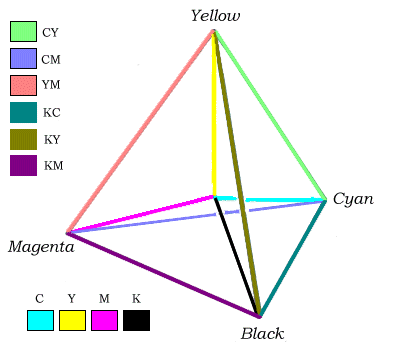
Image by Kirby Urner, published in Color Coordinated Quadrays
The second method of definition of a direction proposed here is reminiscent of fractals. Starting from one triangular sector on the surface of our sphere, we could subdivide it into four equal triangles by joining the mid-points on each one of the three lines connecting the principal axes of the active sector. This would then be repeated, each time narrowing down the area of the vector to be indicated, until the desired granularity and accuracy of indication of the vector has been achieved.

An approximate rendition of the idea would be the Sierpinski triangle. The image above was found on Wikipedia (Sierpinski triangle).
Inward directed pinpoint accuracy
While for the purpose of orientation in space, the tetrahedron is virtualized and calculations must conform to the curved topology of a sphere, it is possible to reverse the vector of observation inward, in which case the tetrahedron itself becomes the important point of reference and Sierpinski's fractalization of it provides us with a means of addressing any point inside with great accuracy.
This could be used to address points inside a crystal, for instance, to laser-stimulate and change memory bits, or for any number of uses you might think of. As an aside, one of the ideas I had in this connection was to achieve laser fusion by directing lasers against a common fusion target from four different directions.
It is my feeling that each one of the proposed methods of description may have its pluspoints and perhaps its drawbacks. Perhaps there are other, completely different methods of mathematically modeling this. It is also possible that two different methods of calculation could be used in combination, fractalization to achieve the desired accuracy and the percentage method to assign the unique color that will permit instantaneous, intuitive orientation.
Help needed
The help I am asking from the more mathematically inclined among you out there, is to comment on these ideas and, if you feel so inclined, to lend a hand elaborating and proposing one or the other - or perhaps a completely different - method of description of vectors based on this tetrahedral system.
To differentiate this idea from the X-Y-Z Cartesian system of co-ordinates, I would like to propose calling this new system the A-B-C-D Tetrahedral system of all-space orientation.
And by the way ... my work is offered as a contribution to the public domain and I would hope that elaborations of mathematical details would be similarly offered in a spirit of an open-source contribution to the commons, although I will not and can not impose that as a condition on anyone.
Related:
Natural Coordinates - by Ray Whitmer
Quadray coordinates - Wikipedia
An Introduction to Quadrays - by Kirby Urner
Color Coordinated Quadrays - by Kirby Urner
Recent:
Curtis Faith took this as the starting point for what he calls "a novel topology for all three of: network topology, physical wireless topology, and organizational structure." He has put his idea down in an entry on his wiki here:
http://inflection-space.wikispaces.com/Support+Technology+Ideas
and adds:
Any physicists or afficionados, please let me know if this seems like an interesting area for potential research in string theory, quantum gravity, or superconductivity.
Please let me know what you think.





This method is better for application in far space. On table or on planet surface people use Decart system since there is vertical line (perpendicular to table): vertical+left+right+force and back... But we have not this simple idea in open far space and simplest case is Tetra Space Coordinates
On Tetrahedral coordinates: Note that the usual xyz coordinate axis can be drawn in an Octahedron, connecting opposite vertices. This is then similar to the Tetra coordinate system you show inside of a Tetrahedron. You should show the usual xyz axis in an Octahedron.
The big advantage to the usual xyz system is that the axis and the 3 planes are orthogonal to one another. (At 90 degrees to one another.) This means that math/vector functions can be decomposed into linearly independent parts. (The part along the x-axis, the part along the y-axis, and these are independent of each other.) That is so very important. It allows for Fourier decomposition of function and Fourier analysis. The Tetrahedral coordinate system needs to demonstrate how to do such analysis without having orthogonal reference axis.
Note that the xyz coordinate system is the way RBFuller mentions that Universe works: That is, Tension and Compression always and only co-exist and operate at 90 degrees to each other, not at tetrahedral angles to each other.
I think the usual xyz system and tetrahedronal system coexist. Don't try to replace one with the other. Show under what conditions the tetrahedral system is easier to use and we'll use it for those special cases. If anyone is serious about rplacing xyz with tetrahedral coordinate system, they need to show how to do Fourier analysis without orthogonal coordinates.
Might then want to look at fractional Fourier transform.
Cheers,
Bob Gray
Good stuff. Right now many of my impressions are general. Definitely we need to set up coordinates in space, and i think this illustration of the relationship between degrees of freedom and the tetrahedron is excellent.
We all need to study Synergetics further. Answers to some of the imprecision of degree measurements can be found in Section 600, which i haven't thoroughly read yet.
Often Fuller discussed 60 degree angles as occurring frequently in natural processes, so we should look in that direction.
As for dimensionality, we haven't really gotten started yet. There seem to be 12 material dimensions and 4 imputed dimensions arising from those. This structure is recapitulated in a matrix of cultures and human sensory systems on this planet, where it was first discovered. It is also found in the Isotropic Vector Matrix, a common natural shape which deserves some careful study.
Some of the commentary in here about dimensions and time made me think of Dewey Larson's Reciprocal Theory.
He started with -- get this! -- "motion" as a primitive/fundamental, and derived "space" and "time" as dimensions from that.
Time, as well as space could have multiple dimensions.
Far out. Truly mind-blowing stuff. Larson also came up with a number of predictions and fascinating thought experiments based on his thinking.
Hi. I have had the opportunity to reflect on the pyramidal coordinates and on some properties of pyramidal geometry. A natural consequence is wave geometry, which is a physical geometry linked with the management of radiation (radiant energy) and with an integrated way of operating with space and time. I developed a small document with what little I learned. If someone wanted to see it, I can share it. Best regards.